Funktionen/Unterroutinen
real(kind=dp) function	rh_zurwitz (model, n, mc)
	gibt die relative Feuchtigkeit passend zur Temperatur und dem Feuchtegehalt nach Zurwitz et. al (Avramidis1989) zurück

real(kind=dp) function	dwdh_zurwitz (model, n, mc)
	gibt 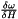$\frac{\delta\omega}{\delta H}$ passend zur Temperatur und dem Feuchtegehalt nach Zurwitz et. al (Avramidis1989) zurück

real(kind=dp) function	emc_zurwitz (model, n, time)

real(kind=dp) function	cdeliiski (model, n, mc)
	Specific Heat capacity according to Olek2003 in .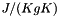

real(kind=dp) function	eb (model, n, mc)
	Activierungsenergie gebundenen Wassers als Funktion des Feuchtegehalt.

subroutine	d_t_beech_ihtp (model, n, T, D_T)
	Heat conductivity tensor of european beech wood according to Olek2003 in .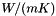

subroutine	d_t_pine_ihtp (model, n, T, D_T)
	Heat conductivity tensor of scots pine wood according to Olek2003 in .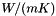

subroutine	d_w_eriksson (model, n, mc, Diffusivity)
	Diffusion Coefficient matrix according to Eriksson2006.

Funktionen/Unterroutinen-Dokumentation

real(kind=dp) function cdeliiski	(	type(model_t), intent(in)	model,
		integer, intent(in)	n,
		real(kind=dp), intent(in)	mc
	)

Specific Heat capacity according to Olek2003 in 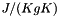$J/(Kg K)$ .

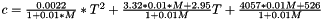
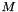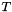$c = \frac{0.0022}{1+0.01*M}*T^2 + \frac{3.32*0.01*M+2.95}{1+0.01M}T+ \frac{4057*0.01M+526}{1+0.01M}$ $M$ in % $T$ in Kelvin

subroutine d_t_beech_ihtp	(	type(model_t)	model,
		integer	n,
		real(kind=dp)	T,
		real(kind=dp), dimension(:,:), pointer	D_T
	)

Heat conductivity tensor of european beech wood according to Olek2003 in 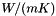$W/(m K)$ .

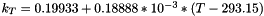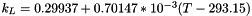
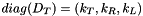
$k_T = 0.19933+0.18888*10^{-3}*(T-293.15)$ k_R = 0.19958+0.33211*10^{-3}(T-293.15) $k_L = 0.29937+0.70147*10^{-3}(T-293.15)$ $ diag(D_T) = (k_T, k_R, k_L)$

subroutine d_t_pine_ihtp	(	type(model_t)	model,
		integer	n,
		real(kind=dp)	T,
		real(kind=dp), dimension(:,:), pointer	D_T
	)

Heat conductivity tensor of scots pine wood according to Olek2003 in 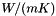$W/(m K)$ .

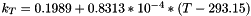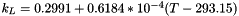
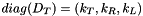
$k_T = 0.1989+0.8313*10^{-4}*(T-293.15)$ k_R = 0.1990+0.8393*10^{-4}(T-293.15) $k_L = 0.2991+0.6184*10^{-4}(T-293.15)$ $ diag(D_T) = (k_T, k_R, k_L)$

subroutine d_w_eriksson	(	type(model_t)	model,
		integer	n,
		real(kind=dp)	mc,
		real(kind=dp), dimension(:,:), pointer	Diffusivity
	)

Diffusion Coefficient matrix according to Eriksson2006.

$D_{} = 2*10^{-9} m^2/s * e^{0.0641+0.04867*}

real(kind=dp) function dwdh_zurwitz	(	type(model_t)	model,
		integer	n,
		real(kind=dp), intent(in)	mc
	)

gibt 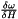$\frac{\delta\omega}{\delta H}$ passend zur Temperatur und dem Feuchtegehalt nach Zurwitz et. al (Avramidis1989) zurück

Zurwitz definiert folgenden Zusammenhang $MC = \left[ -T \frac{ln(1-h)}{c_2 \left(1-\frac{T}{T_c} \right)^{c_1}}\right]^{\frac{1}{c_3 T^{c_4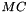}}}$ $MC$ und die Temperatur sind für jeden Knoten bekannt und es folgt nach umstellen: 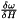$\frac{\delta\omega}{\delta H}$ = {1}{c_3 T^{c_4}}({T}{(1-h)c_2(1-{T}{T_c}^{c_1})^{{1-c_3 T^{c_4}}{c_3 T^{c_4}}

Parameter

n	Knotennummer

Hier ist ein Graph, der zeigt, was diese Funktion aufruft:

real(kind=dp) function eb	(	type(model_t), intent(in)	model,
		integer, intent(in)	n,
		real(kind=dp), intent(in)	mc
	)

Activierungsenergie gebundenen Wassers als Funktion des Feuchtegehalt.

In Eriksson2006 wir für die Aktivierungsenergie gebundenen Wassers

real(kind=dp) function emc_zurwitz	(	type(model_t)	model,
		integer	n,
		real(kind=dp), intent(in)	time
	)

Parameter

n	Knotennummer

real(kind=dp) function rh_zurwitz	(	type(model_t)	model,
		integer	n,
		real(kind=dp), intent(in)	mc
	)

gibt die relative Feuchtigkeit passend zur Temperatur und dem Feuchtegehalt nach Zurwitz et. al (Avramidis1989) zurück

Zurwitz definiert folgenden Zusammenhang $MC = \left[ -T \frac{ln(1-h)}{c_2 \left(1-\frac{T}{T_c} \right)^{c_1}}\right]^{\frac{1}{c_3 T^{c_4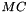}}}$ $MC$ und die Temperatur sind für jeden Knoten bekannt und es folgt nach umstellen: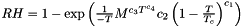 $RH = 1 - \exp{\left(\frac{1}{-T} M^{c_3 T^{c_4}}c_2\left(1-\frac{T}{T_c}\right)^{c_1}\right)}$

Parameter

n	Knotennummer

Hier ist ein Graph der zeigt, wo diese Funktion aufgerufen wird: